动量守恒定律在解决一些力学方面问题时略胜与牛顿运动定律一筹,尤其是在研究火箭等航天航空领域上提供了基础。那么,动量守恒定律是怎么来的,我们如何判断一个物体或系统的动量是否守恒呢?咱们不妨先来看看一个小实验。

在一个光滑的水平面放置着两个质量相等的小车,小车中间有一根弹簧,用细线连接两小车后,弹簧处于压缩状态,此时,整个系统的动量为零。当我们剪短细线后发现,两个小车沿着相反的方向运动,且同时经过与弹簧中心点相同的两个点A点和B点。
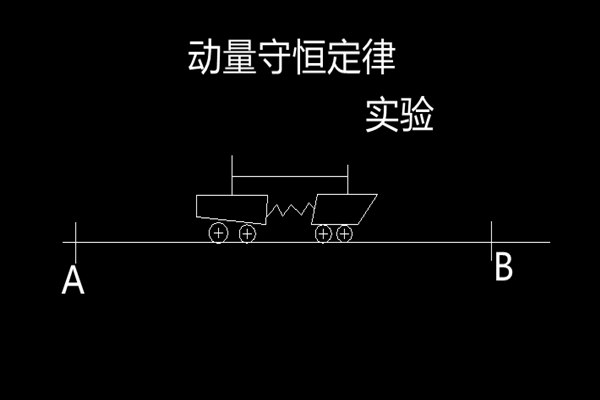
由于动量是适量,当它们同时经过A点和B点时,两个小车的瞬时速度是相等的,也就是说,两个小车的动量大小是相等的,但它们方向相反,故而两个小车也就是系统的动量同样为零。换句话说,它们初末状态的合动量是相等的。从这个实验中就能得出动量守恒定律的两个信息。

第一:系统所受到的合外力为零,毕竟水平面处于光滑状态,也就说系统没有受到摩擦力的作用。
第二:系统所受到的内力远大于系统所受到的外力。
当然,这只是实验观察出来的动量守恒,既然系统的动量守恒,就必须得用一个公式进行表达出来,现在我们来看动量守恒定律的由来吧!

同样是在光滑的水平面上,H球以速度V1向左运动,N球以速度V2也向左运动,假设V2大于V1,那么,在某一时刻,N球是一定会装上H球的。在两小球撞到一起的瞬间,我们设H球受到的撞击力为Fh,N球受到的撞击力为Fn,根据动量定理我们可以列出如下的式子:

即Fh×T=MV1'-MV1,Fn×T=MV2'-MV2,其中V1'为H小球碰撞后的瞬时速度,V2'为N球碰撞后的瞬时速度。再根据牛顿第三定律可知,Fh与Fn是一对作用力与反作用力的关系可得,Fh与Fn的大小是相等且方向相反的。

故而,我们可以得出如下的式子,即MV1'-MV1=-(MV2'-MV2),将等式两边进行处理后就可以得出一个经典的式子,即MV1+MV2=MV1'+MV2',这个式子说明了系统的初动量的合等于末动量的合,这就是著名的动量守恒定律了。

动量守恒定律的运用是有条件的,即系统(两个或两个以上的物体)不受外力或所受到的合外力为零,则系统的动量才守恒。当然,这是绝对理想状态下的情况,当系统受到的外力远小于系统所受到的内力时,我们也可以认为系统的动量同样守恒。现在,我们来说说外力与内力吧!

在这里举一个例子就能一目了然,有根弹簧处于自然伸长状态,弹簧的左边与墙壁相接,右边连接在一个木块上,木块放置在光滑的水平面上,当我们用玩具枪对准木块发射一个飞镖时,飞镖插入木块后将弹簧压缩,在弹簧被压缩至最短距离时,系统的动量守恒吗?
很显然这个系统的动量是不守恒的,因为系统除了受到内力弹力外,还受到了墙壁对系统的支持力(外力),而且这个外力还在时刻发生变化,也就是说系统受到的外力不为零,故而系统的动量不守恒。